Turing Complete Turing Complete ()

SPOILER ネタバレ注意

このガイドでは各問題の答えとなる画像を貼り付けています。spoilerタグで画像を隠す方法もあったのですが、使い勝手が悪かったのでそのままにしています。自力で解いてこそ楽しめる作品だと思いますが、どうしても詰まってしまった、答えを知りたいという場合にご利用ください。

書いていたらなんか参考書チックになってしまったので、勉強みたいでやだなーと思ったら無理して読まなくてOK。分かる範囲で楽しめりゃいいんだよ(ﾟ∀ﾟ)

あと、わかりやすさを重視して、NANDの数が最小になる構成を突き詰めていません。その点ご了承ください。

1. Basic Logic

1-1. Crude Awakening

操作説明。画面左上のINPUTをクリックするとON/OFFを切り替えて動作確認できる。

1-2. NAND Gate

NAND素子の動作確認。動作確認をしながら下の表を埋めればクリア。この素子ひとつで他のすべてを作ることになる。

1-3. NOT Gate

NOT素子を作る問題。

1-4-1. NOR Gate

1-4-2. OR Gate

1-4-3. AND Gate

1-5. Always On

常時ONを出力する素子を作る問題。

1-6. Second Tick

Input1がON、Input2がOFFのときのみONを出力させる問題。

1-7. XOR Gate

1-8-1. Bigger OR Gate

1-8-2. Bigger AND Gate

1-9. XNOR Gate

2. Arithmetic

2-1-1. Double Trouble

4つの入力のうち2つ以上がONになっているときにONを出力させる問題。

解説

1つ目と2つ目がONのとき、1つ目と3つ目がONのとき...という具合に、2つがONになる全パターンをANDで確認すると、脳筋的に判別できる。

2-1-2. ODD Number of Signals

奇数判定の問題。4つの入力のうち奇数個がONになっているときにONを出力させる。

解説

XORのXORをとるといい。偶数+奇数=奇数であることを利用する。

00 00 -> 00 (偶数,偶数) -> 0 (偶数) 00 01 -> 01 (偶数,奇数) -> 1 (奇数) 00 10 -> 01 (偶数,奇数) -> 1 (奇数) 00 11 -> 00 (偶数,偶数) -> 0 (偶数) 01 00 -> 10 (奇数,偶数) -> 1 (奇数) 01 01 -> 11 (奇数,奇数) -> 0 (偶数) ...

2-2-1. Counting Signals

4つの入力のうちONになっている個数を2進数で出力させる問題。

解説

さっきの奇数判別の回路を流用できる。

・1の位は奇数判定の回路と同じ。

・2の位は、1,2と3,4の両方のXORがONのとき、1,2と3,4のうち片方のANDがONのとき、の2パターン考えられるので、それをORでつなげばいい。

確認できるパターン

2個がON: 1010, 1001, 0110, 0101 -> XORを2つとANDで確認

2個がON: 1100, 0011 -> ANDを2つとXORで確認

3個がON: 1110, 1101, 1011, 0111 -> ANDを2つとXORで確認・4の位はすべてがONのときにONを出力するようにAND回路を組めばいい。

2-2-2. Half Adder

半加算器を作る問題。論理回路の問題では必ずと言っていいほど出てくる半加算器。2進数の1桁の足し算の計算結果を出力しよう。

解説

1の位は片方がONのときにONになるのでXOR、2の位は両方がONのときにONになるのでANDを使うといい。表にするとわかりやすい。

00 -> 0,0 01 -> 1,0 10 -> 1,0 11 -> 0,1

2-3-1. Double the Number

1byteの入力を倍にして出力する問題。

解説

1bitずらせば、1が2に、2が4に、4が8に...という具合にすべての桁を2倍にできる。

2-3-2. Full Adder

全加算器を作る問題。半加算器にさらに繰り上がりを足すのを含めたもの。3つの入力の合計を2進数で出力するのが目的。

最大でも全部が1のときに11(つまり3)を出力するのみなので出力は2桁になる。後の問題で出てくるが、繰り上がりを上の桁の計算に入れるように連結することで、桁数の多い足し算ができるようになる。

解説

半加算器を2つ組み合わせて実現する。2つの数字を半加算器に入れて2桁の出力を出した後、下の桁と3つめの数字をさらに半加算器に入れる。

最初の加算では00・01・10のパターンしかないので、繰り上がりが両方1になることはない。そのため、どちらかの加算で繰り上がりが出ていれば繰り上がりを1にすればいい。つまりORで繋ぐ。

0 0 0 -> 00 0 -> 00 0 0 1 -> 00 1 -> 01 0 1 0 -> 01 0 -> 01 0 1 1 -> 01 1 -> 10 1 0 0 -> 01 0 -> 01 1 0 1 -> 01 1 -> 10 1 1 0 -> 10 0 -> 10 1 1 1 -> 10 1 -> 11

2-4-1. Byte OR

2-4-2. Byte NOT

2-4-3. Adding Byte

2つの1byte入力を加算する問題。

解説

10進数の普通の足し算のように、下の桁から足していく。繰り上がりを上の桁の全加算器に入れて、どんどん上の桁を確定させる流れになる。

この問題では、一番上の繰り上がりがあふれるオーバーフローは扱わないらしい。

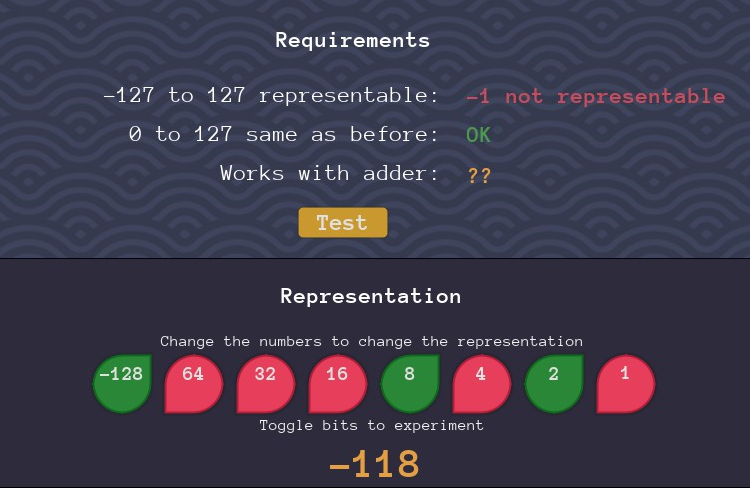
2-5-1. Negative Numbers

負の数の概念が出てくる。

下の8つのbitに適切な数を入力して、-127～127を表現できるようにしよう。

この問題の要求は3つ

1. -127から127を表現できる

2. 0～127はこれまでと変わらない

3. 加算器に通してそのまま計算できる

これを満たすように、各bitに数字を割り当てよう。

解説

127まではそのままという条件があるので、下7bitはそのまま。最後の1bitをどうするかだが、ここに「-128」という数字を割り振ると都合がいい。

いくつか例えを挙げると

-128+ 0 = -128 (1 0000000) -128+ 1 = -127 (1 0000001) -128+ 10 = -118 (1 0001010) -128+127 = -1 (1 1111111) 0 (0 0000000) 10 (0 0001010) 127 (0 1111111) このように、-128～127までを表現できる。

では、加算機に通すとどうなるか。

-15 + 27 = (-128 + 113) + 27 = -128 + 140 = -128 + 128 + 12 = 12 1 1110001 (-15 = -128 + 113) + 0 0011011 (27) = 1 0 0001100 (12) 最上位の桁がオーバーフローして消えてくれるため、正常に計算できる。つまり、上の式で言うと、-128+128=0 という計算が成り立っていることになる。

(-1) + (-1) = (-128 + 127) + (-128 + 127) = -128 - 128 + 254 = -128 - 128 + (128 + 126) = -128 + 126 = -2 1 1111111 (-1) + 1 1111111 (-1) = 1 1 1111110 (-2) 負数どうしの足し算では、もとの-128は消えてしまうが、オーバーフローをしていない限り必ず下の桁からの繰り上がりで-128ができる。つまり-128-128+128=-128の計算が成り立っていることになる。

オーバーフローのしきい値が下がってしまう影響はある。そのため、計算結果が-128～127の範囲を出ないように気をつけなければならない。

127+1 = 128 ---> -128 (0 1111111 + 0 0000001 = 1 0000000)

(-128)+(-1) = -129 ---> 127 (1 0000000 + 1 1111111 = 0 1111111)

2-5-2. Switch

INがONのときにのみ、Inputの信号がOutputに流れる素子を作る問題。

解説

1byteの信号を1bitごとに分解し、INの信号とANDを取ればいい。

2-6. Signed Negator

符号を反転させて、正の数を負の数に、負の数を正の数に変換する問題。

解説

結論だけ書くと、Byte NOTで反転させて、1を足せばいい。

大雑把にだが説明しよう。

符号を反転させた数とはなにか。元の数と足すと0になる数のことだ。

元の数の下位7bitを a、符号を反転させた数の下位7bitを b とおくと、

元の数が正の数の場合、(0 + a) + (-128 + b) = 0 となればいい

元の数が負の数の場合、(-128 + a) + (0 + b) = 0 となればいい

どちらの場合も、変形すると a + b = 128 となる

２進数に直すと、a + b = 10000000

2進数の計算で、足して 10000000 を作るのを考えるのは難しいが、

ここで、10000000 = 1111111 + 0000001 (128 = 127 + 1)ということを利用する。

2進数の足し算で、ある数から 1111111 (127) を作るのは簡単だ。

NOTで反転した数字と足せばいい。

0011010 (26) + 1100101 (101) = 1111111 (127) 繰り上がりがないので、これが明らかなのはわかると思う。

つまり、a をNOTで反転して1111111になる数字をつくり、それに1を足した数が a と足すと10000000になる数字、つまり b になる。

次に最上位bitを考える。

符号を反転させた数は、元の数から最上位bitを反転させたものだ。

というわけで、すべてのbitを反転させて、1を足せばよい。

(説明に不備があるが、全部書くと長くなるので気になったら調べてみてください)

2-7. Demux

INがOFFのときに上の出力をON、INがONのときに下の出力をONにする問題。

解説

0,1の信号を、0のときに1になる線と、1のときに1になる線に分ける回路。

これを作るの自体は簡単だが、のちに大きい回路を作るときに役に立つ。

2-8. Bigger Demux

2進数の入力を分解する問題。1が入力されたときに1番目の端子をONに、8が入力されたときに8番目の端子をONにしよう。

解説

3つの端子を持つANDを使って力押してで解ける。さっきのDemuxを使って、各bitが0と1それぞれのときに別の線に出力させて、000のとき、001のとき、010のとき...と計8種類、各場合をAND回路で拾っていけば簡単だ。

2-9. One Way

信号の逆流を防ぐ端子を作る問題。

解説

信号の逆流や混線を防ぐための端子。もともとNAND素子自体にその機能がある。NAND素子から作ったNOT素子を2つ並べるのが一番シンプルだろう。

3. Memory

3-1. Circular Dependency

自己参照・循環参照を作る問題。

解説

自己参照・循環参照を起こすと信号が高速で切り替わって回路が焼ききれてしまう場合があるので、通常のステージでは禁止されている。

上の例で言うと、NOTの手前がOFFなのでONを出力する、すると手前もONになるのでOFFを出力する、すると...と瞬間的に高速にON・OFFが切り替わって破損する。

3-2. Tangled Gates

3-3. Understanding the Flip Flop

3-4. Bit Inverter

3-5. Saving Gracefully

3-6. Input Selector

3-7. Saving Bytes

3-8-1. Little Box

3-8-2. Counter

4. CPU Architecture

4-1. Logic Engine

解説

一見大掛かりな回路だが、これは1byteのAND演算をする素子がなかったせい。本体はAND・NAND・OR・NORを切り替えるだけの回路。

4-2-1. Arithmetic Engine

解説

上のLogic EngineにADD(加算)・SUB(減算)を付け加えたもの。A-Bの減算をするには、BをマイナスにしてAと足せばいい。

どの信号がどのMUXの切り替えに使われているか把握できればOK。

4-2-2. Registers

Copy命令を実装して、CPUの基礎を作る問題。

解説

CPUを作ると聞くと厳ついイメージがあるが、やることは割と単純。レジストリ(1byteのメモリ)のSave・Loadを操作して、レジストリどうしや入出力端子の間を数値を移動させる。

まずは各入力と出力をぐるっと繋ぐ。次に命令コードを1bitの信号に分解、各レジストリのSaveとLoad・入出力のONとOFFに繋げばそれで完成。配線もシンプル。

DEMUXは、3bitの0～7の信号を、8つの端子のON/OFFの信号に変換する素子。「2-8. Bigger Demux」で作ったそのままのもの。

4-3. Component Factory

自由な素子を作れるサンドボックスのステージ。解くべき問題は用意されておらず、そのまま先に進める。

4-4. Decoder

4-5. Calculations

命令の上位2bitでComputeが指示されたときに、REG1とREG2の数値に対して下位6bitで指定された演算をして、REG3に結果を格納する。

解説

レジストリの出力を下手に繋ぐと信号が混線してしまうため、常時出力のあるRegister Plusを使うと楽。

ALU(上の「4-2-1. Arithmetic Engine」で作った計算回路)に1byteの命令とREG1とREG2の常時出力を常に繋いでおき、Compute命令が出たときに結果をREG3に流し、REG3にSaveさせよう。

逆流防止の素子を繋いでいるのは、Copy命令が出たときにSave端子から命令が逆流してくるため。

4-6-1. Conditions

4-6-2. Program

4-7. Immediate Value

4-8. Turing Complete

5. Programming

5-1. Masking Time

CPUを作って終わりではない。ここからは実際に動かすことになる。

この問題では、Inputからの入力を4で割った余りを出力するのが目標。

プログラムメモリの右上のEditボタン(鉛筆マーク)で命令を編集できる。ダイアログ下側のInstructionsを押すと、どのbitをONにすればどんな命令になるか確認できる。

10 110 001 (Copy Input Reg1) 00 000011 (Immediate 3) 10 000 010 (Copy Reg0 Reg2) 01 000 011 (Compute AND) 10 011 110 (Copy Reg3 Output) 解説

4で割った余りを求めるにはAND演算を使えばよい。上の5行のプログラムで処理できる。

入力に00000011をAND演算すると、4の桁=4の倍数、8の桁=4の倍数、16の桁=4の倍数...と、4の倍数の数字を切り落とし、余りである1の桁と2の桁だけを切り出せる。

上で設計したように、Immediate命令の数値はREG0に格納され、Compute命令はREG1とREG2の数値の演算結果をREG3に格納する。うまくCopy命令をつかって数値を移動させよう。

5-2. Calibrating Laser Cannon

隕石の半径から円周の長さを求める問題。π=3で計算していいということで、2πr=6π、つまりInputの入力を6倍にして出力すればいい。

今回からは右のようなダイアログで、バイトコードに1対1で命令を割り当てて、それを使ってコードを書くことができる。自分で使いやすい名前を割り当てよう。

input_1 (Copy Input Reg1) cp_1_2 (Copy Reg1 Reg2) add (Compute Add) cp_3_1 (Copy Reg3 Reg1) add (Compute Add) cp_3_1 (Copy Reg3 Reg1) cp_3_2 (Copy Reg3 Reg2) add (Compute Add) output_3 (Copy Reg3 Output) 解説

((x+x)+x)*2 = 6x という計算

5-3. Special Invasion

今度はロボットを動かしてスペースインベーダーのようなことをする問題。ロボットの動かし方については右のような解説が追加される。

0～6の数字の出力で上下左右への方向転換と移動・足踏み・前方のオブジェクトの検知・レーザーの発射ができるほか、矢印キーやスペース,Ctrlなどで動作を試すこともできる。レーザーでインベーダーのように動く16体の宇宙ネズミを倒そう。

なお、レーザーは画面上に既にある場合、追加で発射することができない。

6 (Immediate 6) output_0 (Copy Reg0 Output) - Shoot laser 3 (Immediate 3) output_0 (Copy Reg0 Output) - Move up 5 (Immediate 5) output_0 (Copy Reg0 Output) - Use action input_3 (Copy Input Reg3) 4 (Immediate 4) jump_eq0 (Condition ≠0) 6 (Immediate 6) output_0 (Copy Reg0 Output) - Shoot laser output_0 (Copy Reg0 Output) - Shoot laser output_0 (Copy Reg0 Output) - Shoot laser output_0 (Copy Reg0 Output) - Shoot laser 4 (Immediate 4) jump (Condition Always) 解説

Condition命令のお試し問題と言ってもいい内容。上で設計した通り、ConditionはReg3の数値を判定して、成立していればReg0の値をプログラムカウンタにコピーするので、Immediate命令で予めReg0にジャンプ先の行数を入れておくとよい。

また、Outputに直接好きな数字を送ることができないため、一旦Immediate命令でReg0に数字を入れ、Reg0からOutputにCopyしている。

インベーダー宇宙ネズミどもを倒すのに今回取った手順だが、

1. 最初に目の前の壁をぶち壊して一歩前に出る

2. 目の前を探索して入力を得て、0(なにもない)ならその場でループする

3. 0でないならレーザーを4回撃つ

こういう作戦だ。

5-4. The Maze

プログラムの題材としてはお決まりの、迷路を探索する問題。上下左右への方向転換と、前方のマスの判定を利用して左上のゴールに辿り着こう。

解説

この手の問題ではおなじみの、左手伝いに辿ればゴールに辿り着く法則を使う。

1. 前方を調べて、壁ならば、その場で右に方向転換して1.を繰り返す

2. 壁でなければ前進

3. 前進をしたあとに左に方向転換

4. 1に戻る

この手順で実行できる。

このロボットは、向いている方向とは別の方向の入力があった場合、まずその場で方向転換し、向いている方向と同じ入力があってはじめてその方向に前進する性質がある。

前進や右折・左折というコマンドがないため、現在向いている方向を覚えておく必要がある。これは、Copy以外の命令による上書きがない汎用レジスタであるReg4やReg5を活用することで実現できる。

また、方向の入力は0～3で、右・下・左・上と割り当てられているため、4を越えると4で割って余りを得る必要がある。ちょうど「5-1. Masking Time」で使ったばかりのANDを利用すればよい。

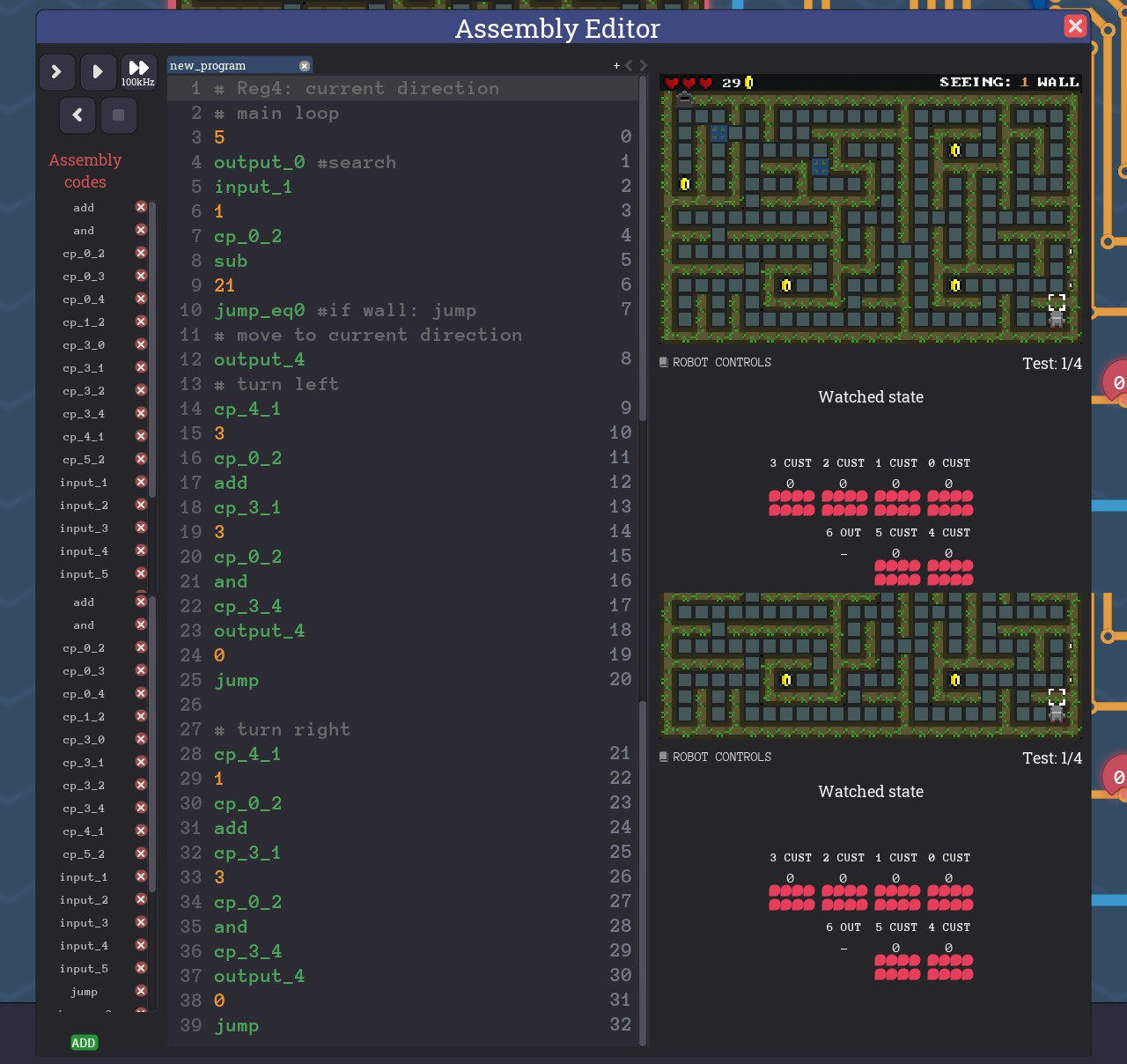
右への方向転換は1足して4で割った余りを入れればいいが、左への方向転換に1を引くと負の数が出てくる。そのため、3を足して4で割った余りを入れることで代用してみた。

なお、このコードではReg4の初期値0を利用することで、最初にReg4に数値を代入する手間を省いていることに注意。# Reg4: current direction # main loop 5 output_0 #search input_1 #(Copy Input Reg1) - 0: Empty, 1: Wall, 8: Gold 1 cp_0_2 sub 21 jump_eq0 #if wall: jump # move to current direction output_4 #(Copy Reg4 Output) # turn left cp_4_1 3 cp_0_2 add #Reg1 + 3 cp_3_1 3 cp_0_2 and #Reg1 modulo 4 cp_3_4 output_4 0 jump # turn right cp_4_1 1 cp_0_2 add #Reg1 + 1 cp_3_1 3 cp_0_2 and #Reg1 modulo 4 cp_3_4 output_4 0 jump

6. CPU Architecture 2

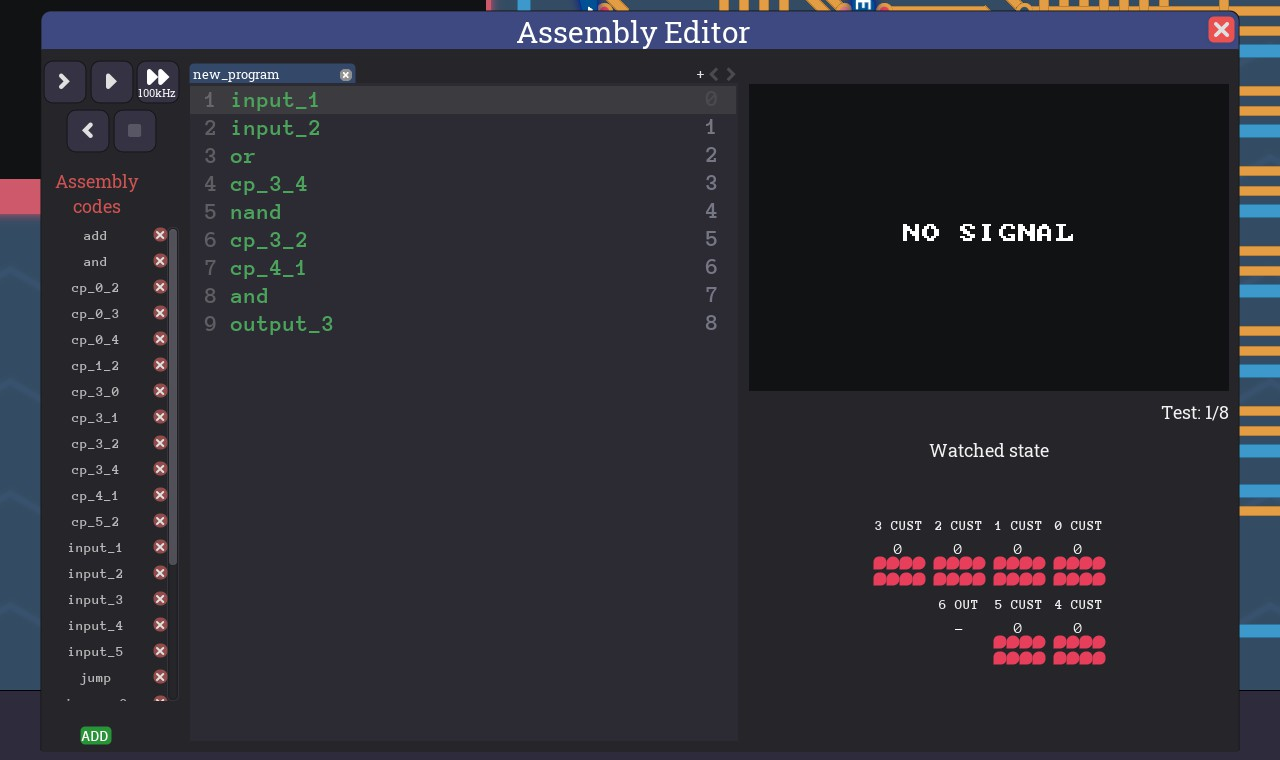
6-1-1. XOR

6-1-2. Byte Constant

6-1-3. Byte AND

6-2-1. Byte XOR

6-2-2. Equality

6-3. Less

6-4. Wide Instructions

6-5. Wire Spaghetti

6-6. Opcodes

6-7. Immediate Values

6-8. Conditionals

7. Functions

7-1-1. Shift

7-1-2. The Lab

7-1-3. Delay

7-2-1. The Product of Nibbles

7-2-2. RAM

7-3-1. Divide

7-3-2. Stack

7-4. PUSH and POP

7-5. Functions

8. Assembly Challenges

8-1-1. Planet Names

8-1-2. Tower of Radioactive Alloy

8-1-3. Unseen Fruit

8-1-4. Delicious Order

8-2-1. Water World

8-2-2. Robot Racing

8-2-3. AI Showdown

8-3. Dancing Machine

Source: https://steamcommunity.com/sharedfiles/filedetails/?id=2625107424

Turing Complete ()