0. Purpose Of Writing This Guide
This walkthrough is written for anyone who needs some basics of computer science and mathematical logic to clear all levels, especially I will describe the objectives for each section of levels and how to use the component factory to make components that help us build two types of CPU architecture: Overture and LEG.
I’d like this guide to get into the knowledge underlying this puzzle game. I hope I can make this guide more informative and suitable for all non-specialized readers interested in logic and computer science. Without further ado, let’s get started!
*This guide is temporary and being updated. I will divide this long guide into smaller ones section by section.
1. Basic Logic
ObjectiveIn this section the player is asked to make different kinds of logic gates with NAND gates so that the player can use logic gates to make the building blocks of functional units (e.g. arithmetic logic units and memory).
Solutionhttps://steamcommunity.com/sharedfiles/filedetails/?id=3078668306
2. Arithmetic And Memory
ObjectiveIn this section the player is asked to use logic gates and other components to build an arithmetic logic unit (ALU) and memory as the building blocks of CPU architecture.
Solutionhttps://steamcommunity.com/sharedfiles/filedetails/?id=3078986482
1.1 Truth Table
A truth table is a table that assigns each combination of truth values of all variables in an expression with logical operator(s) to a truth value. The following are the truth tables of three common logical operators: NOT, AND and OR.
Negation (NOT): the opposite of the truth value of a variable (denoted by x')
xNOT1001Conjunction (AND): true if both two variables are true (denoted by xy)
xyAND111100010000Disjunction (OR): true if one of two variables is true (denoted by x+y)
xyOR111101011000Notes: If no parenthesis is used, the priority of operation always follows the order: negation, conjunction, disjunction and from left to right if in the same order. For example, xy'z+x' equals ((x(y'))z)+(x').
1.2 Boolean Algebra
Boolean algebra is a binary operation structure that consists of logical variables, constants 0 and 1, and logical operations AND, OR and NOT satisfying the following properties:
Associativity(xy)z=x(yz)(x+y)+z=x+(y+z)Commutativityxy=yxx+y=y+xAbsorptionxy+x=x(x+y)x=xDistributivityxy+z=(x+z)(y+z)(x+y)z=xz+yzComplementsxx'=0x+x'=1Idempotencexx=xx+x=xBoundednessx1=x, x0=0x+0=x, x+1=1Double negationx''=xDe Morgan's laws(xy)'=x'+y'(x+y)'=x'y'In the game, we can optimize our design by using the properties above to minimize the number of logic gates and delay. For example, we can use the distributive property to reduce the number of logic gates we use from three to two.
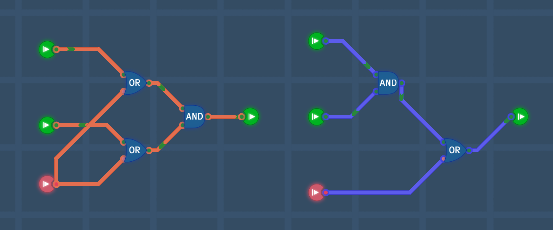
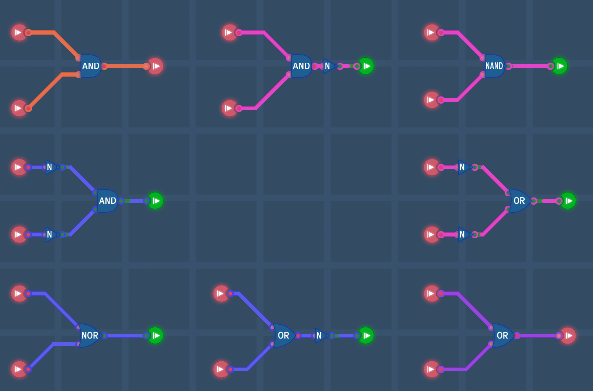
De Morgan's laws allow us to convert AND, OR, NAND, or NOR gates into another. Circuits in the same color are logically equivalent (have the same truth value). Output is inverted when we convert gates between left and right. Input is inverted when we convert gates between top and bottom.
1.3 Analysis Of Logic Circuits
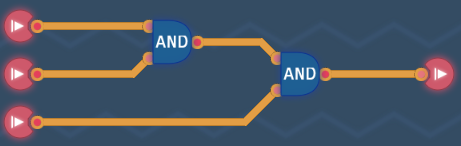
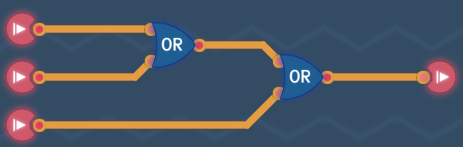
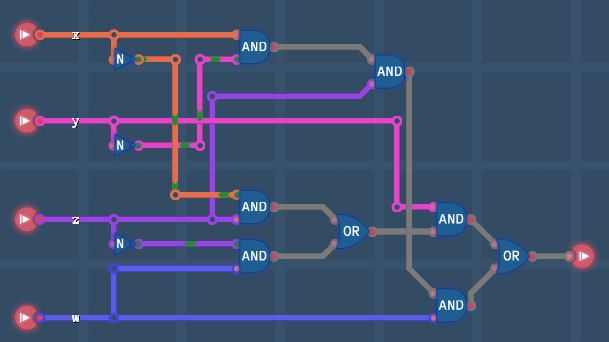
Control of conditionsFor every logic circuit, we can use AND or OR gates to accurately control the circuit's conditions, which means we can freely assign which combinations of truth values to 1. Due to the associative and commutative property, the order of operations and inputs has no effect on the result of a circuit when any number of AND gates (or OR gates) are used individually. So,
Use AND gates when all conditions are required.
Use OR gates when one of conditions is required.
Karnaugh map and Boolean sum of productsA Karnaugh map is the truth table used for the simple analysis of a logic circuit with two up to four inputs. The head of rows or columns of a Karnaugh map represents every possible combination of truth values of input (usually pairs of input appears in the head of either rows or columns) respectively. Each intersection of a row and a column represents the truth value to which the corresponding combination is assigned. For example, in a four-variable Karnaugh map,
x,y\z,w00011011000000010111100001110100The truth value in the third row and the fourth column shows the output is 1 when the input x,y,z,w are 1,0,1,1 respectively. So we can write down the conjunction of each condition of input:
xy'zwSimilarly we have the rest of all conditions that make the output be 1:
x'yz'w
x'yzw'
x'yzw
xyz'wFinally we get the Boolean sum of products of this truth table by writing down the disjunction of all the conjunctions listed above:
x'yz'w+x'yzw'+x'yzw+xy'zw+xyz'wSimplification of a Boolean expressionLet A be a Boolean expression and let b be a logical variable. Based on the operation laws, we have
Ab+Ab'=A(b+b')=A1=ATherefore we can simplify the expression of any form Ab+Ab' to A. For example, in the sum of products mentioned above, we have
x'yzw'+x'yzw=x'yz (A=x'yz, b=w)
x'yz'w+xyz'w=yz'w (A=yz'w, b=x)Replace the original terms with these, we have
x'yz+xy'zw+yz'wBased on the distributive property, we can simplify the terms containing either y or w as needed. If we want to simplify the terms containing y, we have
y(x'z+z'w)+xy'zwThis logic circuit requires three NOT gates, six AND gates and two OR gates. Readers can check the result by themselves.
Although Boolean sums of products cannot guarantee the optimal design, it helps us figure out designs that satisfy the condition of complex logic circuits.
2.1 Binary Number
A binary number is a number whose digits are either 0 or 1 and represent the multiple of powers of 2. The Nth digit of a binary number from the right represents the multiple of the (N-1)th power of 2. If a,b,c are digits of a binary number abc, then
abc=a*2^2+b*2^1+c*2^0=4a+2b+cHence the number 7 in base 10 can be represented as 111 in base 2 because 7=4+2+1. Every number in base 10 can be converted into a binary number by expressing its series of powers of 2.
2.2 Bits And Bytes
Bits are binary digits. They are also the units of information that describe two equally possible states, such as 0 or 1. A bit of information is equal to the amount of information we need to determine which side faces up when we flip a coin. Bytes are bundles of eight bits, so a byte has 2^8=256 equally possible states. Larger units of byte are kilobytes (KB), megabytes (MB) and gigabytes (GB).
2.3 Short Circuit
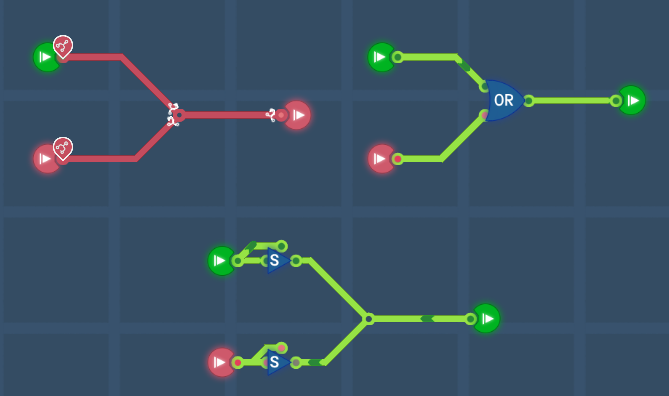
A short circuit is a circuit in which a wire directly connects two nodes at different voltage, such as a wire that directly connects two terminals of a battery. In a logic circuit, a short happens when a wire connects two different inputs. It is one of the most common errors to be avoided in a circuit design. Using OR gates or bit switches can avoid this type of error.
2.4 Delayed Line
In a logic circuit, a delayed line is a component that creates a time difference between input and output for a signal to take. Although a delay is undesirable in most times because it reduces the efficiency of signal transmission, it can help us save signals for a long time for future use.
2.5 Loop

A loop is a closed path in a circuit, so the input of each component in a loop depends on its output. This usually causes chaos in a logic circuit because both input and output are indeterminate. It is one of the most common errors to be avoided in a circuit design as well. However, the construction of a loop is allowed if there is a delayed component placed in that loop because the signal flow to the input is delayed and does not affect the output in the same tick.
2.6 Vertical Algorithm Of Addition
A common way to do the addition of two numbers by hand is to line up two numbers digit by digit and add up two digits in each column in turn starting from the right. A carry is the extra digit of the sum of two digits in a column when the sum reaches or exceeds the base (base 2 for bits). Then the carry is added to the sum of two digits in the next column. So, there are three digits to be added up after the first column: two digits in the column and a carry from the previous column.
568+273=71311+11=841This is called the vertical algorithm of addition. This algorithm underlies how a full adder works.
2.7 Representation Of Negative Numbers
For any signed number, we have to reserve a place to denote the sign. For a binary number, the easiest way to do so is simply using the highest bit to denote the sign. But we also need to find a good way for a computer to handle both signed and unsigned numbers at the same time.
Modular arithmeticModular arithmetic is arithmetic involving the operations on remainders of integers with the same divisor (whole numbers divided by the same number). Let a,b are integers to be divided and n is a divisor. If the remainders of a and b are equal, then we say a is congruent to b modulo n, denoted by a=b (mod n). Modular addition has a remarkable property: the remainder of the sum of two integers is equal to the remainder of the sum of the remainders of the two integers. That is
(a+b) mod n = (a mod n + b mod n) mod nSo we can replace a and b with any congruent integer. For example, a 3-bit number can express eight numbers from 0 to 7. Any number less than 0 or greater than 7 can only be expressed by its remainder on the clock. For 5+4=9, 101+100=1001 in base 2, the remainder of 9 divided by 8 is 1, which corresponds to the first three digits 001 in 1001 in base 2. Similarly, because -3 is congruent to 5 and 20 is congruent to 4, 20-3=17 is congruent to 5+4=9, which is congruent to 1.
Two's complementTherefore, we can regard the upper half of the eight numbers 4-7 as -4 to -1 and the lower half 0-3 remains the same with no change of the clock arithmetic. That is the same as the change in the highest digit from 4 to -4. If we need to calculate 3-1=2, we only need to calculate 3+7=10. Because 10 is congruent to 2, the result of 3-1 is 2. Similarly, to calculate 2-3=-1, we have 2+5=7. Because 7 represents -1, the result of 2-3 is -1. To find the opposite of a number x, we have
-x=0-x=8-x=(7+1)-x=(7-x)+1 (mod 8)Because 7 is 111 in base 2, any 3-bit number subtracted from 111 is the bitwise negation of itself (0 becomes 1 and 1 becomes 0 after the subtraction). Therefore the opposite of an N-bit number (except for -2^(N-1)) is the sum of the bitwise negation of the number itself and 1. This method of representing the opposite of a binary number is called two's complement.
2.8 Encoders And Decoders
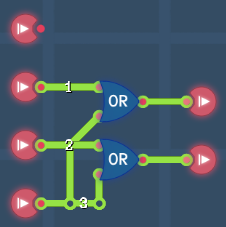
Encoders are electronic components used to convert 2^N lines of signals to N-bit numbers. Decoders work in the opposite way of what encoders do. They convert N-bit numbers to 2^N lines of signals. As shown in the left figure, the four inputs on the left from top to bottom represent 0 to 3 and are encoded to 00, 01, 10 and 11, respectively. The two outputs on the right from top to bottom represent 1's and 2's place of a 2-bit number. Although encoders are unnecessary for all levels, they may inspire the player to create complex CPU architecture in the sandbox.
2.9 Arithmetic Logic Unit
An arithmetic logic unit (ALU) is a computational unit that performs arithmetic and bitwise operations on binary numbers. To do a computation, binary numbers and a code that indicates the operation should be put in an ALU. Addition is one of the most common operations in ALUs. The other common operations in ALUs include subtraction, bitwise AND, OR and NOT.
2.10 Memory
Computer memory is a unit that saves data and programs. Based on different uses, computer memory can be classified into registers, primary and secondary memory. A register is a type of memory that holds data for immediate use in a series of calculations. The storing time and space of a register is normally short and limited. Primary memory is a type of memory that can store data relatively longer and more than a register for immediate use in the computer, but it can't be used to exchange data between two different computers. Instead, secondary memory is a type of memory responsible for the long-term storage of a large amount of data, such as hard drives and CDs. We can attach secondary memory to a computer when we need to save or load data.
2.11 Counter
A counter is used to record the address of a code in a program. When we want a computer to execute a specific code in a program, we need to know the address of that code and set the counter to that address. Like a register, we can overwrite the counter or load the number saved in the counter to control the path of the execution of a program.
3. CPU Architecture
ObjectiveIn this section the player will use the components created in the last section to construct a CPU: Overture, including the installation of registers, counters, programs, calculations and conditions.
3.1 Component Factory
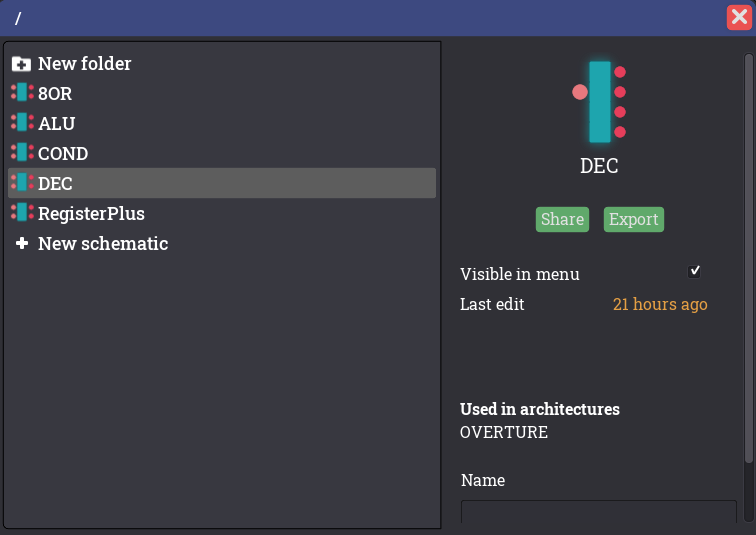
The component factory is the workbench for the player to create components that can be used to construct complex architectures. The shape of a component depends on its layout. The player is allowed to relabel input and output and use a probe to display the signal inside a component. In order to create a new component, go to the schematic menu and name the new schematic. Then double click the schematic the player wants to edit.
3.2 Condition
A condition is a logical operation that determines whether a binary number satisfies an equation or inequality. In CPU architecture, conditions can be used to control the execution of a program by jumping to the address of the code the player wants to execute. This can be done by overwriting the counter. The basic properties of equations or inequalities are listed below:
Law of trichotomy: If x,y are integers, then x<y, x=y or x>y.
If x,y are integers, then
Reflexivityx=xSymmetryIf x<y, then y>xIf x=y, then y=xIf x>y, then y<xTransitivityIf x<y and y<z, then x<zIf x=y and y=z, then x=zIf x>y and y>z, then x>zIf x,y,a are integers, then
Ifx<yx=yx>yAll ax+a<y+ax+a=y+ax+a>y+aa<0ax>ayax=ayax<aya=0ax=ay=0ax=ay=0ax=ay=0a>0ax<ayax=ayax>ayWe can use these properties to simplify an equation or inequality in order to execute the condition instruction we've already made. For example, to determine if x=5, we can rewrite this equation into x-5=0. Then we can put the instruction "=0" and the input "x-5" in a condition unit.
3.3 Program
A program is a set of instruction codes to be executed. The address of each instruction code is recorded by a counter. In the next section the player will perform simple programming tasks. For example, if the player wants to add two numbers from input a and b, the player should first write two codes that allow a CPU to copy each input to register 1 and 2. Then write a code to carry out the addition, and then write the last code to output the result saved in register 3.
3.4 Immediate Value
Immediate values are codes stored in a program in contrast to values saved in memory. For example, if the player wants to put a number in a register, the player can use the immediate value mode and directly write the number the player wants to copy in the program.
3.5 Turing Completeness
A data-instruction system is Turing complete if it can simulate any Turing machine, which is an imaginary machine that can read symbols in the squares of an infinitely long tape. A Turing machine can write a new symbol, move the tape or change its state based on its current state or symbol. The following shows how a Turing machine carries out the two's complement of a binary number ("NOT" is the initial state and the first digit from the left is the initial position).
Current stateCurrent symbolOverwriting symbolMove directionNext stateNOT01RightNOTNOT10RightNOTNOTBlankBlankLeftAdd 1Add 101LeftResetAdd 110LeftAdd 1Add 1BlankBlankRightHaltReset00LeftResetReset11LeftResetResetBlankBlankRightHaltFor the binary number 10100, we have
Step 0Blank10100BlankNOT,1Step 1Blank00100BlankNOT,0Step 2Blank01100BlankNOT,1Step 3Blank01000BlankNOT,0Step 4Blank01010BlankNOT,0Step 5Blank01011BlankNOT,BlankStep 6Blank01011BlankAdd 1,1Step 7Blank01010BlankAdd 1,1Step 8Blank01000BlankAdd 1,0Step 9Blank01100BlankReset,1Step 10Blank01100BlankReset,0Step 11Blank01100BlankReset,BlankStep 12Blank01100BlankHalt,0The result is 01100, as expected.
3.X Solution
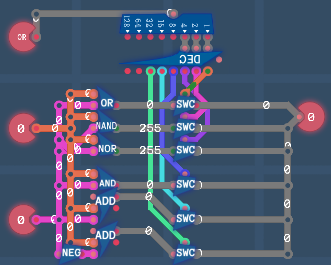
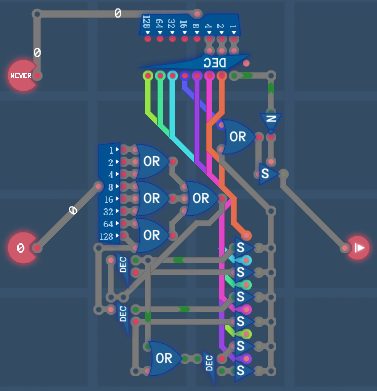
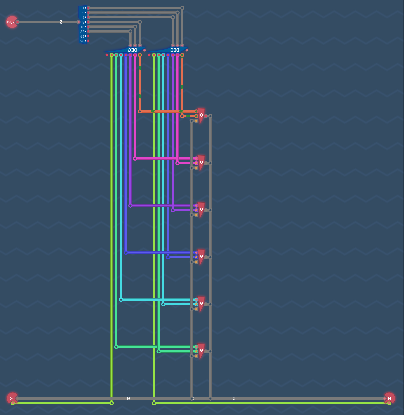
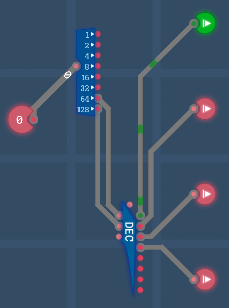
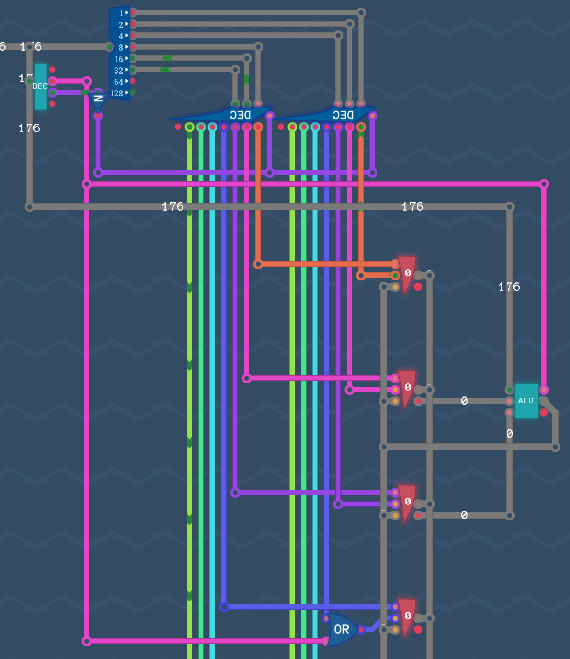
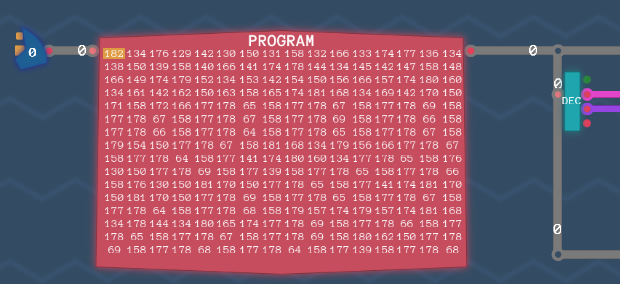
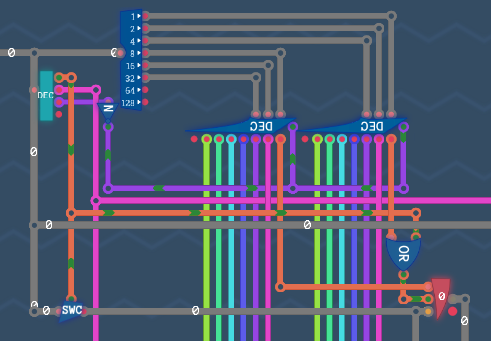
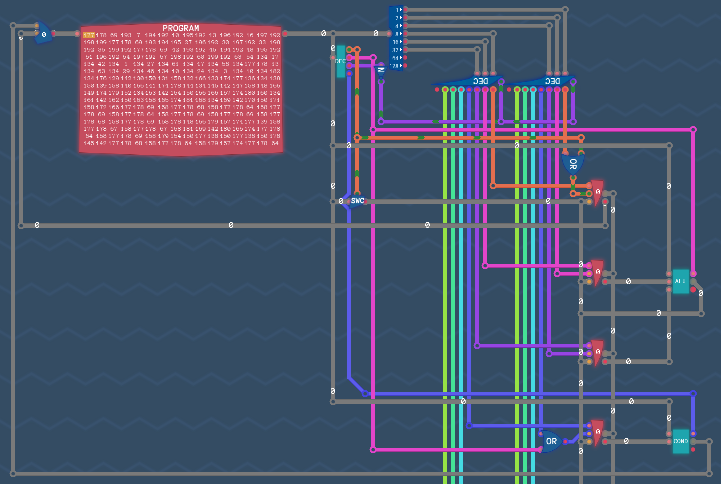
Notes: The layout of each component used in the following figures is shown in Section X.
Arithmetic EngineConditionsRegistersInstruction DecoderCalculationsProgramImmediate ValuesTuring Complete
4. Programming
ObjectiveIn this section the player needs to be familiar with simple programming tasks and the use of assembly language by editing the programming memory of the CPU created in the last section.
4.1 Instruction Manual

In the game, the instruction manual allows the player to record a list of instruction codes to be executed. The list depends on the design of CPU architecture. To record a new instruction code, click the downward arrow to expand the list, click the plus sign to add a line, toggle each symbol of a byte (green denotes ON, red denotes OFF and gray with a question mark denotes either ON or OFF), and then edit the label by changing its range or name. Once the player adds a new instruction code, toggle the symbols on the panel in order to match the bit pattern of the new code.
4.2 Assembly Language
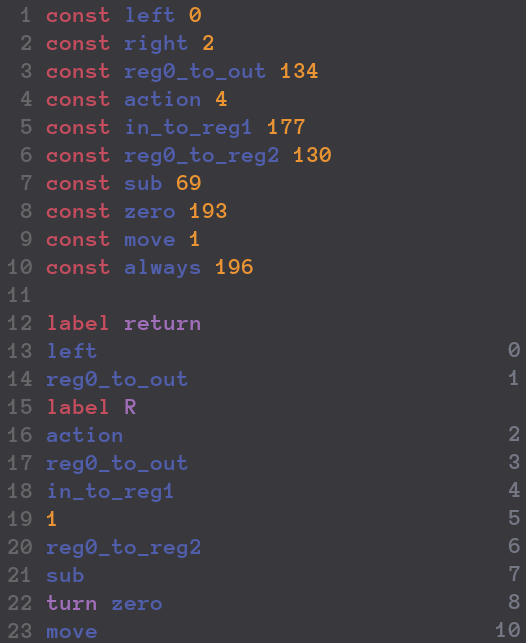
Assembly language (a.k.a. symbolic machine code) is a list of names of instruction codes in the programming memory of a CPU, in contrast to bits or bytes. Using assembly language in programming is convenient for programmers to understand the algorithm of a task. For example, instead of typing a number defining addition, we can define the string "add" as that number in advance and then type the string "add" directly while coding.
When completing a programming level in the game, the player can type "const 'string' 'number' " to define a string as a number. For example, one can type "const add 68" to let "add" be "68".
The player can also use "label" to label a code address when a program needs to jump to that specific code if a condition is met. For example, one can type "label 'string' " to refer a string to a code address and then type " 'string' 'condition' " to execute the jump if the condition defined by the code is met. Otherwise, the program will normally execute the next line of code.
4.X Solution

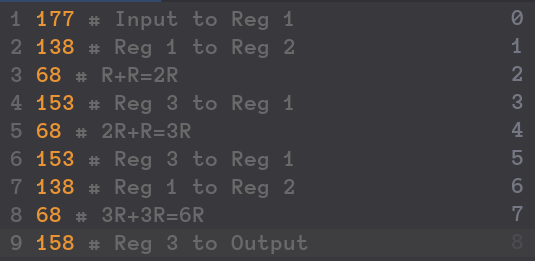
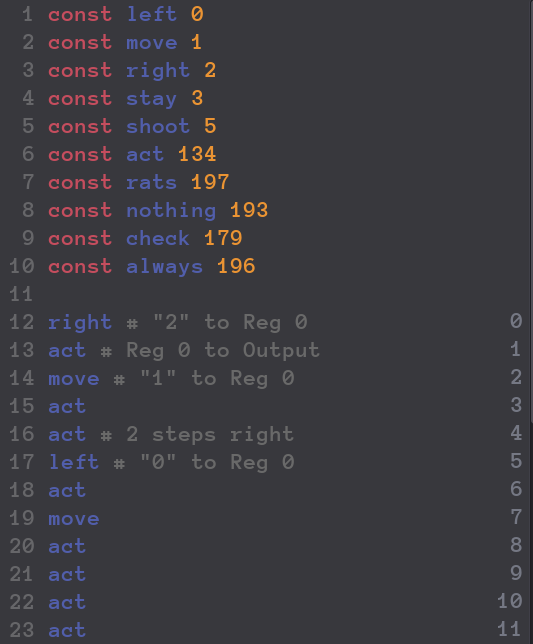
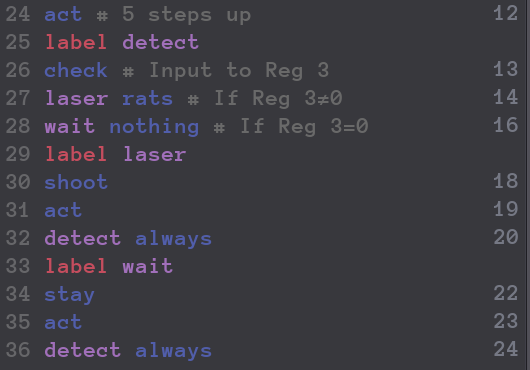
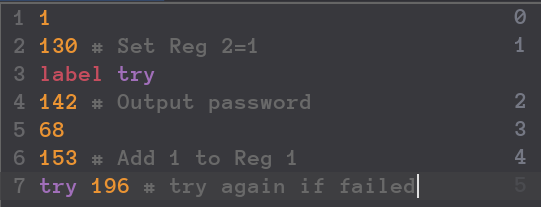
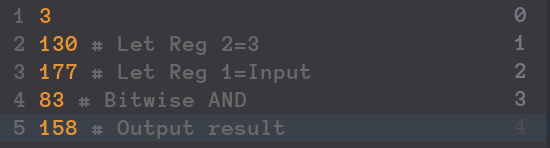

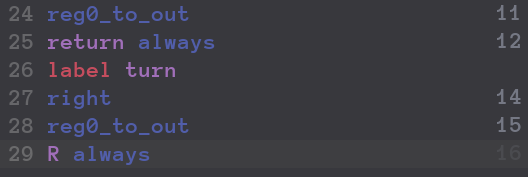
Add 5Calibrating Laser CannonsSpacial InvasionStorage CrackerMasking TimeThe Maze
5. CPU Architecture 2
Objective
5.1 Binary Operation
5.2 LEG Architecture
5.X Solution
huh
X. Component Preparation
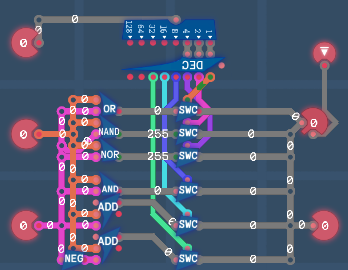

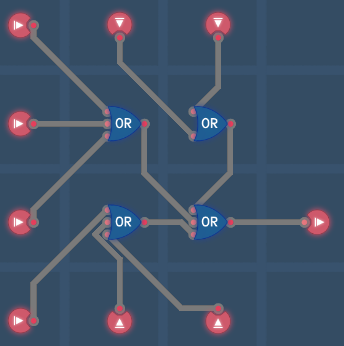
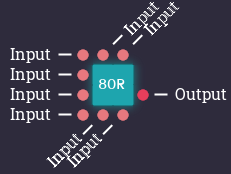
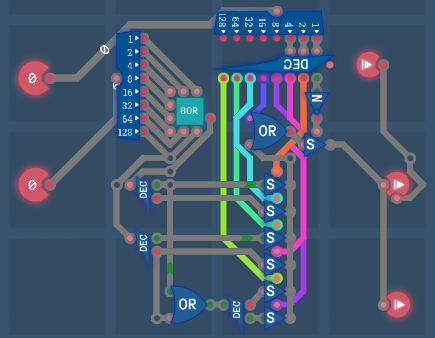



Arithmetic Logic Unit (ALU)8-Input ORCondition UnitInstruction Decoder
Source: https://steamcommunity.com/sharedfiles/filedetails/?id=3058316651
More Turing Complete guilds
- All Guilds
- Turing Complete Guide 202
- Turing Complete: Basic Logic-Manual
- Robot Racing
- Turing Complete: Basic Logic-Solution
- Turing Complete: CPU Architecture-Solution
- Turing Complete: Arithmetic and Memory-Solution
- The 6502 Microprocessor
- Turing Complete Guide 157
- / Turing Complete
